2.2　筛选法模拟的实验范例

模拟过程中可能产生的所有解组成一个筛。筛选法模拟即先从题意中找出约束条件，然后将筛中的每一个可能解放到约束条件的过滤器上，一次一次地将不符合条件的解过滤掉，最后沉淀在筛中的即为问题的解。

筛选法模拟的结构和思路简明、清晰，但带有盲目性，因此时间效率并不一定令人满意。筛选法模拟的关键是找准约束条件，任何错误和疏漏都会导致模拟失败。【2.2.1　The Game】【问题描述】五子棋游戏是由两名玩家在一个19*19的棋盘上玩的游戏。一名玩家执黑，另一名玩家执白。游戏开始时棋盘为空，两名玩家交替放置黑色棋子和白色棋子。执黑者先走。棋盘上有19条水平线和19条垂直线，棋子放置在直线的交点上。水平线从上到下标记为1，2，…，19，垂直线从左至右标记为1，2，…，19。这一游戏的目标是把5个相同颜色的棋子沿水平、垂直或对角线连续放置。所以，在图2.2-1中执黑的一方获胜。但是，如果一个玩家将超过五个相同颜色的棋子连续放置，也不能判赢。　

基于这一游戏的棋盘情况，请写一个程序，确定是白方赢了比赛，还是黑方赢了比赛，或者是还没有任何一方赢了比赛。输入数据保证不可能出现黑方和白方都赢的情况，也没有白方或黑方在多处获胜的情况。 输入： 输入的第一行包含一个整数t(1≤t≤11)，表示测试用例的数目。接下来给出每个测试用例，每个测试用例19行，每行19个数，黑棋子标识为1，白棋子标识为2，没有放置棋子则标识为0。 输出： 对每个测试用例，输出一行或两行。在测试用例的第一行输出结果，如果黑方获胜，则输出1；如果白方获胜，则输出2；如果没有任何一方能获胜，则输出0。如果黑方或白方获胜，则在第二行给出在5个连续的棋子中最左边棋子的水平线编号和垂直线编号（如果5枚连续的棋子垂直排列，则选最上方棋子的水平线编号和垂直线编号）。

试题来源：ACM Tehran Sharif 2004 Preliminary

在线测试地址：POJ 1970，ZOJ 2495试题解析初始时所有棋子组成一个筛子。我们由上而下、由左而右扫描每个棋子，分析其k方向的相邻棋子(0≤k≤3，0≤i,j≤18，见图2.2-2)。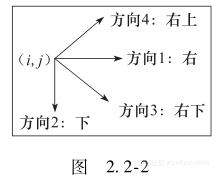　

过滤器中“赢”的约束条件是： 1）（i，j）k的相反方向的相邻格（x,y）不同色。 2）（i，j）k方向延伸5格在界内。 3）从（i，j）开始，沿k方向连续5格同色且第6格不同色。 若（i，j）的棋子满足上述约束条件，其颜色所代表的一方赢，（i，j）即为赢方5个连续的同色棋子中首枚棋子的位置；若检测了4个方向，（i，j）的棋子依然不满足约束条件，则被过滤掉。 若过滤了筛中的所有棋子后筛子变空，则说明没有任何一方能获胜。 程序清单

#include 
    
     using namespace std;const int d［4］［2］ = {
   {0, 1}, {1, 0}, {1, 1}, {-1, 1}};　　// 4个方向的位移增量inline bool valid(int x, int y)// 返回（x，y）在界内的标志{return x >= 0 && x < 19 && y >= 0 && y < 19;}int a［20］［20］;// 五子棋盘int main(){int i, j, k, t, x, y, u;scanf("%d", &t);// 输入测试用例数while (t--)// 反复输入测试用例{for (i = 0; i < 19; ++i)// 输入五子棋盘for (j = 0; j < 19; ++j) scanf("%d", &a［i］［j］);for (j = 0; j < 19; ++j)// 由左而右、由上而下扫描每个有棋子的// 位置（i，j）{for (i = 0; i < 19; ++i){if (a［i］［j］ == 0) continue;for (k = 0; k < 4; ++k)// 枚举4个方向{// 过滤：若（i，j）k的相反方向的相邻格// （x，y）同色，则换一个方向；若（i，j）k方向延伸5格越出界外，则换一个方向；若（i，j）k方向的连续6个格子同色，// 则换一个方向x = i - d［k］［0］;y = j - d［k］［1］;if (valid(x, y) && a［x］［y］ == a［i］［j］) continue;x = i + d［k］［0］ *4;y=j + d［k］［1］ *4;if (!valid(x, y)) continue;for (u = 1; u < 5; ++u){x = i + d［k］［0］ *u;y = j + d［k］［1］ *u;if (a［x］［y］ != a［i］［j］) break;}x = i+d［k］［0］*5;y = j+d［k］［1］*5;if (valid(x, y) && a［x］［y］ == a［i］［j］) continue;if (u == 5) break;}if (k < 4) break;}if (i < 19) break;}if (j < 19)// 若（i，j）在某方向上存在连续5个同色// 格，则该色一方赢；若扫描了所有格子仍未出现任何方向上有连续5个同色格的情况，则没有任何一方能获胜{printf("%d＼n", a［i］［j］);// 输出赢方的标志和5个连续棋子的起始// 位置printf("%d %d＼n", i + 1, j + 1);}else puts("0");// 输出没有任何一方能获胜的信息}return 0;}
    

【2.2.2　Game schedule required】

【问题描述】Sheikh Abdul真正热爱足球，所以你最好不要问他为著名的球队进入年度锦标赛花了多少钱。当然，他花了这么多钱，就是想看到某些球队彼此间的比赛。他拟定了他想看到的所有比赛的完整列表。现在请按以下规则将这些比赛分配到某些淘汰赛的轮次中：在每一轮中，晋级的每支球队最多只进行一场比赛。如果有偶数支晋级这一轮的球队，那么每支球队只进行一场比赛。如果有奇数支晋级这一轮的球队，那么恰好有一支球队没有进行比赛（它优先用外卡晋级下一轮）。每场比赛的优胜者晋级下一轮，失败者被淘汰出锦标赛。如果只有一支球队，那么这支球队就被宣布为锦标赛的优胜者。可以证明，如果有n支球队参加锦标赛，那么直至产生比赛优胜者，恰好有n-1场比赛。显然，在第一轮后，有的应该要参加下一轮比赛的球队可能会被淘汰，为了防止这种情况，对于每场比赛，还必须知道哪支球队会赢。输入：输入包含若干测试用例，每个测试用例首先给出一个整数n（2≤n≤1000），表示参加锦标赛的球队的数目。然后的n行给出参加锦标赛的球队的队名。本题设定每个球队的队名可以由多达25个英文字母的字符组成（'a'～'z'或'A'～'Z'）。接下来的n-1行给出Sheikh想要看的比赛（按任何顺序）。每行由要进行比赛的两支球队的队名组成。本题设定总是可以找到一个包含给出比赛的锦标赛日程。测试用例结束后，给出一个0。输出：对于每个测试用例，输出一个分布在多个轮次中的比赛日程。对于每一轮，首先在一行中输出"Round #X"(其中X表示第几轮)，然后输出在这一轮中的比赛形式："A defeats B"，其中A是晋级队的队名，B是被淘汰队的队名。如果在这一轮需要外卡，则在这一轮最后一场比赛后，输出"A advances with wildcard"，其中A是获得外卡的球队的队名。在最后一轮之后，按如下格式输出优胜队，在每个测试用例之后输出一个空行。

试题来源：Ulm Local 2005

在线测试地址：POJ 2476，ZOJ 2801试题解析可能的赢方组成一个筛子，初始时每个球队在筛中。我们首先计算Sheikh想要看的n-1场比赛中每场比赛的两个球队编号a［i］和b［i］（1≤i≤n-1）,累计每个球队比赛的场次数cnt［i］（1≤i≤n）。然后从第一轮次开始，计算分布在每个轮次中比赛的日程。由于每一轮的比赛都是Sheikh想要看的，因此若当前比赛的两个球队中仅有一个球队没有比赛完，则该球队赢。由此得出过滤器中“保留球队”的约束条件：1）Sheikh想要看的比赛中的两个球队不在当前轮次。2）当前轮次Sheikh想要看的比赛中需要进入下一轮的球队。满足上述条件的球队留在筛中。在进入第一轮前，所有球队都在筛中。每个轮次的比赛场次数为进入该轮次前筛中的球队数2。反复进行如下过滤，直至筛中仅剩一支球队为止：顺序搜索Sheikh想要看的每场比赛i（1≤i≤n-1）：若a［i］和b［i］在筛中，且两队中至少有一支队伍只能比一场，则这两个球队比赛1场，两队剩余的比赛场次数-1；在筛中滤去这两个球队（避免球队在当前轮次比赛两场）。若仅存在1个可进入下一轮的球队，则该队赢本场比赛；若两队都不能进入下一轮，则产生锦标赛的优胜者。若比赛完当前轮次的所有场次，则新增一个轮次，新轮次的比赛场次数为筛中的球队数2，向筛中还有比赛的球队发放外卡，筛外未比赛完的球队重新回到筛里，以进入新一轮。程序清单

#include
    
     #include
     
      #include
      
       #include
       
        #include
        
         #include
         
          #include